3.1 Arcball Camera Control

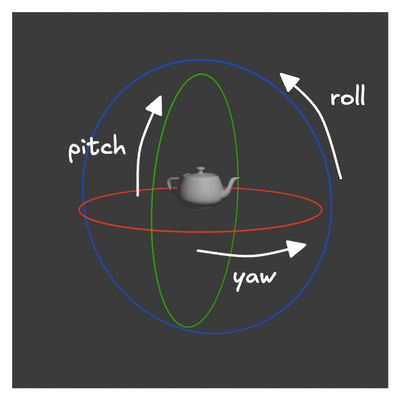
Another common interaction in 3D rendering is the ability to rotate the 3D object. This is often implemented using a concept called Arcball. The idea is simple: we enclose the 3D object inside a virtual 3D sphere and use the mouse to rotate this sphere. While the mouse cursor moves in a 2D plane, it controls the 3D rotation of the sphere. But how can 2D movement control 3D rotation? In 3D space, rotation can occur in three different directions: roll, pitch, and yaw.

We handle this by projecting our virtual sphere onto the screen plane. When the mouse cursor moves within the projected area, the x-axis movement controls yaw, and the y-axis movement controls pitch. If the mouse cursor moves outside the projected area, we rotate the object along the roll direction.

In this demo, we visualize the projected sphere by drawing a ring that highlights the silhouette of the sphere. Rendering this ring is a standard operation seen many times in this book, so I will skip the details here. Please refer to the sample code for implementation details.

One thing to note when rendering this ring is that we use the line-strip type for the geometry primitive in the pipeline.

For visualization, we will render the same teapot as before, but this time, we can rotate it freely. Again, I will skip the details as it is almost the same as before.

For the Arcball, we encapsulate its implementation in a class:

class Arcball {
    constructor() {
        this.radius = 5.0;
        this.forwardVector = glMatrix.vec4.fromValues(this.radius, 0.0, 0.0, 0.0);
        this.upVector = glMatrix.vec4.fromValues(0.0, 0.0, 1.0, 0.0);
        this.currentRotation = glMatrix.mat4.create();
    }
    yawPitch(originalX, originalY, currentX, currentY) {

}
roll(originalX, originalY, currentX, currentY) {

}
getMatrices() {

    }
}

Let me explain the class members. The radius is the distance between the focal point, or the rotation center, and the camera. The forwardVector defines the viewing direction from the camera's position to the focal point. It is initialized with (radius, 0.0, 0.0), meaning the camera starts at (radius, 0.0, 0.0) and looks at the origin. The upVector is perpendicular to the forwardVector and points upward from the camera's perspective.

The Arcball

The currentRotation is the rotation matrix of our Arcball.

yawPitch(originalX, originalY, currentX, currentY) {
    let originalPoint = glMatrix.vec3.fromValues(1.0, originalX, originalY);
    let newPoint = glMatrix.vec3.fromValues(1.0, currentX, currentY);

    let rotationAxis = glMatrix.vec3.cross(glMatrix.vec3.create(), originalPoint, newPoint);

    rotationAxis = glMatrix.vec4.fromValues(rotationAxis[0], rotationAxis[1], rotationAxis[2], 0.0);

    rotationAxis = glMatrix.vec4.transformMat4(glMatrix.mat4.create(), rotationAxis, this.currentRotation);

    rotationAxis = glMatrix.vec3.normalize(glMatrix.vec3.create(), glMatrix.vec3.fromValues(rotationAxis[0], rotationAxis[1], rotationAxis[2]));

    let sin = glMatrix.vec3.length(rotationAxis) / (glMatrix.vec3.length(originalPoint) * glMatrix.vec3.length(newPoint));

    let rotationMatrix = glMatrix.mat4.fromRotation(glMatrix.mat4.create(), Math.asin(sin) * -0.03, rotationAxis);

    if (rotationMatrix !== null) {
        this.currentRotation = glMatrix.mat4.multiply(glMatrix.mat4.create(), rotationMatrix, this.currentRotation);
        this.forwardVector = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), this.forwardVector, rotationMatrix);
        this.upVector = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), this.upVector, rotationMatrix);
    }
}

The first function we examine controls the yaw and pitch. This function takes two inputs: the original mouse position (originalX, originalY) and the current mouse position (currentX, currentY) in screen space. Initially, the camera is positioned at (radius, 0, 0), so the plane parallel to the screen is the yz-plane. The first step is to project the original and current points in screen space to the yz-plane: (1.0, originalX, originalY) and (1.0, currentX, currentY). We use coordinates (1.0, ...) instead of (radius, ...) to simplify calculations by treating our imaginary sphere as having a radius of 1. This simplification does not affect correctness because we perform calculations in the sphere's coordinate system.

Next, we need to calculate the axis around which we will apply the rotation. This axis is perpendicular to the plane formed by the original and current vectors, so we get it by performing a cross product of the two vectors.

The above calculation assumes there is no previous rotation in the system, meaning the yz plane is still aligned with the screen plane. If there have been previous rotations, we need to apply these rotations to the rotation axis. Finally, we normalize this rotation axis to a unit vector.

Next, we need to obtain the rotation angle, derived by first calculating the sine value and then using the arcsine function. The maximum rotation angle is less than 90 degrees.

Finally, we calculate the rotation matrix using the axis and the rotation angle. In the code, we check if the rotation matrix is null because, when the original and current vectors are very close, numerical instability might result in an invalid rotation matrix.

If we have a valid rotation matrix, we then merge the existing rotation with the new rotation matrix and use them to rotate the camera's forward and up vectors.

roll(originalX, originalY, currentX, currentY) {
    const originalVec = glMatrix.vec3.fromValues(originalX, originalY, 0.0);
    const currentVec = glMatrix.vec3.fromValues(currentX, currentY, 0.0);

    const crossProd = glMatrix.vec3.cross(glMatrix.vec3.create(), originalVec, currentVec);


    let rad = glMatrix.vec3.dot(glMatrix.vec3.normalize(glMatrix.vec3.create(), originalVec),
        glMatrix.vec3.normalize(glMatrix.vec3.create(), currentVec));

    if (rad > 1.0) {
        // cross product can be larger than 1.0 due to numerical error
        rad = Math.PI * Math.sign(crossProd[2]);
    }
    else {
        rad = Math.acos(rad) * Math.sign(crossProd[2]);
    }

    let rotationMatrix = glMatrix.mat4.fromRotation(glMatrix.mat4.create(), -rad, this.forwardVector);
    if (rotationMatrix !== null) {
        this.currentRotation = glMatrix.mat4.multiply(glMatrix.mat4.create(), rotationMatrix, this.currentRotation);
        this.upVector = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), this.upVector, rotationMatrix);
    }
}

The second function to examine is the roll function. This function is triggered when the mouse cursor is dragged outside the ring. For rolling, the rotation axis is always perpendicular to the screen plane, either pointing toward the viewer or away from them. Therefore, we perform our calculations in the screen plane's coordinates, making the original and current vectors (originalX, originalY, 0.0) and (currentX, currentY, 0.0) respectively.

We calculate the cross product to get the rotation axis. Ideally, this axis should be either (0, 0, 1) or (0, 0, -1), but only the last component matters for determining the rotation direction.

For the rotation angle, we calculate it using the dot product and the arccosine function. Numerical errors might result in the dot product being slightly larger than 1, which would cause the arccosine function to return NaN. To prevent this, we treat the rotation angle as either \pi or -\pi in such cases. Otherwise, we use the arccosine value for the angle and the sign of the last component of the rotation axis to determine the direction.

Finally, we convert the rotation angle into a rotation matrix. Although the calculations are performed in the screen plane, we apply the rotation in the camera's coordinate system. Since the rotation axis for rolling is the same as the camera's forward vector, we create the rotation matrix using the forward vector and the rotation angle.

Once we have the rotation matrix, we merge the existing rotation with the new rotation matrix and update the upVector since rolling doesn't change the forwardVector.

getMatrices() {
    let modelViewMatrix = glMatrix.mat4.lookAt(glMatrix.mat4.create(),
        glMatrix.vec3.fromValues(this.forwardVector[0], this.forwardVector[1], this.forwardVector[2]),
        glMatrix.vec3.fromValues(0, 0, 0), glMatrix.vec3.fromValues(this.upVector[0], this.upVector[1], this.upVector[2]));

    return modelViewMatrix;
}

Finally, in the Arcball class, we need a function to get the modelViewMatrix according to the updated forward and up vectors. We can achieve this by calling the lookAt helper function provided by glMatrix. When rendering our 3D object, we just need to call this function to get the modelViewMatrix.

Next, let's look at how to handle the mouse events:

let prevX = 0.0;
let prevY = 0.0;
let isDragging = false;
const yawPitch = 1;
const roll = 2;

canvas.onmousedown = (event) => {
    var rect = canvas.getBoundingClientRect();
    const x = event.clientX - rect.left;
    const y = event.clientY - rect.top;

    const width = rect.right - rect.left;
    const height = rect.bottom - rect.top;
    let radius = width;

    if (height < radius) {
        radius = height;
    }

    radius *= 0.5;
    const originX = width * 0.5;
    const originY = height * 0.5;

    prevX = (x - originX) / radius;
    prevY = (originY - y) / radius;
    if ((prevX * prevX + prevY * prevY) < 0.64) {
        isDragging = yawPitch;
    }
    else {
        isDragging = roll;
    }
}

In the mousedown event handler, our main goal is to determine the type of movement: yawPitch or roll. Recall that if the cursor is within the projected sphere, we will perform yaw and pitch; if it is outside, we perform roll. Here’s an explanation of what this function does, section by section:

var rect = canvas.getBoundingClientRect();
const x = event.clientX - rect.left;
const y = event.clientY - rect.top;

const width = rect.right - rect.left;
const height = rect.bottom - rect.top;

These lines are a common formula to get the mouse cursor position within a canvas, using the top left corner as the origin.

let radius = width;

if (height < radius) {
    radius = height;
}

radius *= 0.5;

These lines select the minimum of the width and height, halve it, and use it as the radius. We do this to ensure the projected sphere fits within the screen area, so the radius can be as large as the shorter side of the screen.

const originX = width * 0.5;
const originY = height * 0.5;

prevX = (x - originX) / radius;
prevY = (originY - y) / radius;

These lines transform the coordinate system from using the top left corner as the origin to using the center of the screen plane as the origin. We flip the Y axis because the canvas coordinate system has the y-axis pointing downwards, whereas the screen coordinate system has it pointing up.

We also normalize the coordinates by the radius because we want the rotation sensitivity to be unaffected by the size of the canvas.

if ((prevX * prevX + prevY * prevY) < 0.64) {
    isDragging = yawPitch;
}
else {
    isDragging = roll;
}

Finally, we calculate the distance from the mouse cursor to the screen center and use a fixed threshold of 0.64 to determine the rotation type. If the cursor falls within 0.8 of the shortest side of the canvas, we consider it yaw and pitch; otherwise, it is roll.

canvas.onmousemove = (event) => {
    if (isDragging != 0) {

        if (isDragging == yawPitch) {
            arcball.yawPitch(prevX, prevY, currX, currY);
        }
        else if (isDragging == roll) {
            arcball.roll(prevX, prevY, currX, currY);
        }
        prevX = currX;
        prevY = currY;
        requestAnimationFrame(render);
    }
}

canvas.onmouseup = (event) => {
    isDragging = 0;
}

Next, let’s examine the mousemove function. What’s omitted in the above function snippet is similar to the mousedown function, hence I only show the differences here. We call the corresponding rotation functions based on the previously determined rotation type. After that, we request a new frame to be rendered.

I will skip the rendering code as there is nothing special here. All we need to do for rendering is to obtain the latest modelViewMatrix from the Arcball class and update all necessary uniform buffers, such as the normal matrix.