4.1 Radix Sort
Prefix sum is a crucial foundation for numerous parallel algorithms. In this chapter, we explore its role in constructing another fundamental element: a sorting algorithm known as radix sort. This sorting technique will be instrumental in our next chapter, where we apply it to implement Gaussian splatting.
The goal of radix sort is to arrange key-value pairs based on their keys, where each key is an integer. This sorting process involves examining one digit of all keys at a time. For instance, if all keys are decimal numbers less than 100, each key has two digits. During sorting, we first consider the least significant digit and rearrange the entire list based on that digit alone. Next, we move on to the most significant digit and reorder the list again. It's important to note that each step of reordering must be a stable sort. This means that if two elements have the same key, the one that appeared earlier in the input will also appear earlier in the sorted output. By ensuring this stability, the order established during the first pass based on the least significant digit can be maintained while performing subsequent passes. Therefore, once we have sorted the list digit by digit, we can be confident that the final list will be ordered by the key.
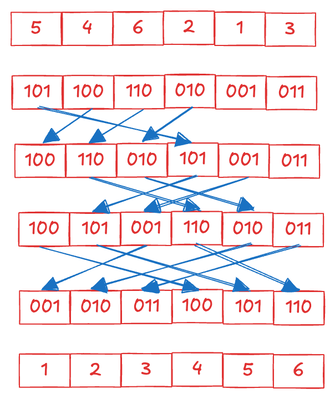
How is radix sort related to prefix sum? Let's illustrate this relationship using an even simpler case: binary keys. When our keys are binary, with only two possible values (zero and one) for each digit, sorting by a single digit is akin to performing a prefix sum on the occurrences of zeros and ones. Once we have computed the prefix sum, we can predict the new position in the sorted list for each element. For instance, if an element is zero and we know the prefix sum k of all zero occurrences, the element's new location in the sorted list should be k+1. Similarly, if an element is one and we know the prefix sum w of all one occurrences, the element's new location should be w+1+z, where z is the count of all zeros.
This approach can be readily extended to digits of a different numeral system, such as decimal. However, there's a trade-off to consider when selecting the numeral system. Using a system with fewer possible values for a digit, like binary, results in keys with more digits. Consequently, more iterations are needed to complete the sorting process. Conversely, opting for a system with more values per digit shortens the key length but requires more prefix sums in each iteration and more storage to keep track of them. In our example, we will use the Quaternary numeral system.
What has been described so far is the basic concept. In practice, however, there are additional considerations, primarily due to the 256-workgroup size limit, which means we can only work on arrays of up to size 512. For longer lists, we need to divide the list into multiple 512-sized chunks. To address this, we divide our sorting algorithm into three phases.
In the first phase, we compute prefix sums within each chunk and save the results, which we refer to as local prefix sums. Additionally, we write the total count of all possible digit values into a global list.
The second phase involves computing another set of prefix sums on this global list.
The final phase is the shuffling phase. Here, based on the local prefix sums and the global digit value count, we determine the sorted position of each element in the resulting array and write the value to that location.
To completely sort a list, we must repeat the three-phase process described above for the entire length of the key's digits.
@binding(0) @group(0) var<storage, read> input :array<u32>;
@binding(1) @group(0) var<storage, read_write> output :array<vec4<u32>>;
@binding(2) @group(0) var<storage, read_write> sums: array<u32>;
@binding(0) @group(1) var<uniform> radixMaskId:u32;
const bank_size:u32 = 32;
const n:u32 = 512;
var<workgroup> temp0: array<u32,532>;
var<workgroup> temp1: array<u32,532>;
var<workgroup> temp2: array<u32,532>;
var<workgroup> temp3: array<u32,532>;
fn bank_conflict_free_idx( idx:u32) -> u32 {
var chunk_id:u32 = idx / bank_size;
return idx + chunk_id;
}
@compute @workgroup_size(256)
fn main(@builtin(global_invocation_id) GlobalInvocationID : vec3<u32>,
@builtin(local_invocation_id) LocalInvocationID: vec3<u32>,
@builtin(workgroup_id) WorkgroupID: vec3<u32>) {
var thid:u32 = LocalInvocationID.x;
var globalThid:u32 = GlobalInvocationID.x;
var mask:u32 = u32(3) << (radixMaskId << 1);
if (thid < (n>>1)){
var val:u32 = (input[2*globalThid] & mask) >> (radixMaskId << 1);
if (val == 0) {
temp0[bank_conflict_free_idx(2*thid)] = 1;
}
else if (val == 1) {
temp1[bank_conflict_free_idx(2*thid)] = 1;
}
else if (val == 2) {
temp2[bank_conflict_free_idx(2*thid)] = 1;
}
else if (val == 3) {
temp3[bank_conflict_free_idx(2*thid)] = 1;
}
val = (input[2*globalThid+1] & mask) >> (radixMaskId << 1);
if (val == 0) {
temp0[bank_conflict_free_idx(2*thid+1)] = 1;
}
else if (val == 1) {
temp1[bank_conflict_free_idx(2*thid+1)] = 1;
}
else if (val == 2) {
temp2[bank_conflict_free_idx(2*thid+1)] = 1;
}
else if (val == 3) {
temp3[bank_conflict_free_idx(2*thid+1)] = 1;
}
}
workgroupBarrier();
var offset:u32 = 1;
for (var d:u32 = n>>1; d > 0; d >>= 1)
{
if (thid < d)
{
var ai:u32 = offset*(2*thid+1)-1;
var bi:u32 = offset*(2*thid+2)-1;
temp0[bank_conflict_free_idx(bi)] += temp0[bank_conflict_free_idx(ai)];
temp1[bank_conflict_free_idx(bi)] += temp1[bank_conflict_free_idx(ai)];
temp2[bank_conflict_free_idx(bi)] += temp2[bank_conflict_free_idx(ai)];
temp3[bank_conflict_free_idx(bi)] += temp3[bank_conflict_free_idx(ai)];
}
offset *= 2;
workgroupBarrier();
}
if (thid == 0)
{
temp0[bank_conflict_free_idx(n - 1)] = 0;
temp1[bank_conflict_free_idx(n - 1)] = 0;
temp2[bank_conflict_free_idx(n - 1)] = 0;
temp3[bank_conflict_free_idx(n - 1)] = 0;
}
workgroupBarrier();
for (var d:u32 = 1; d < n; d *= 2) // traverse down tree & build scan
{
offset >>= 1;
if (thid < d)
{
var ai:u32 = offset*(2*thid+1)-1;
var bi:u32 = offset*(2*thid+2)-1;
var t:u32 = temp0[bank_conflict_free_idx(ai)];
temp0[bank_conflict_free_idx(ai)] = temp0[bank_conflict_free_idx(bi)];
temp0[bank_conflict_free_idx(bi)] += t;
t = temp1[bank_conflict_free_idx(ai)];
temp1[bank_conflict_free_idx(ai)] = temp1[bank_conflict_free_idx(bi)];
temp1[bank_conflict_free_idx(bi)] += t;
t = temp2[bank_conflict_free_idx(ai)];
temp2[bank_conflict_free_idx(ai)] = temp2[bank_conflict_free_idx(bi)];
temp2[bank_conflict_free_idx(bi)] += t;
t = temp3[bank_conflict_free_idx(ai)];
temp3[bank_conflict_free_idx(ai)] = temp3[bank_conflict_free_idx(bi)];
temp3[bank_conflict_free_idx(bi)] += t;
}
workgroupBarrier();
}
if (thid == 0) {
var count0:u32 = temp0[bank_conflict_free_idx(2*255)];
var count1:u32 = temp1[bank_conflict_free_idx(2*255)];
var count2:u32 = temp2[bank_conflict_free_idx(2*255)];
var count3:u32 = temp3[bank_conflict_free_idx(2*255)];
var last:u32 = (input[2*((WorkgroupID.x+1) * 256-1)] & mask) >> (radixMaskId << 1);
switch(last) {
case 0: {count0 += 1;}
case 1: {count1 += 1;}
case 2: {count2 += 1;}
case 3: {count3 += 1;}
default {}
}
last = (input[2*((WorkgroupID.x+1) * 256-1)+1] & mask) >> (radixMaskId << 1);
switch(last) {
case 0: {count0 += 1;}
case 1: {count1 += 1;}
case 2: {count2 += 1;}
case 3: {count3 += 1;}
default {}
}
sums[WorkgroupID.x * 4] = count0;
sums[WorkgroupID.x * 4+1] = count1;
sums[WorkgroupID.x * 4+2] = count2;
sums[WorkgroupID.x * 4+3] = count3;
}
if (thid < (n>>1)){
output[2*globalThid].x = temp0[bank_conflict_free_idx(2*thid)];
output[2*globalThid+1].x = temp0[bank_conflict_free_idx(2*thid+1)];
output[2*globalThid].y = temp1[bank_conflict_free_idx(2*thid)];
output[2*globalThid+1].y = temp1[bank_conflict_free_idx(2*thid+1)];
output[2*globalThid].z = temp2[bank_conflict_free_idx(2*thid)];
output[2*globalThid+1].z = temp2[bank_conflict_free_idx(2*thid+1)];
output[2*globalThid].w = temp3[bank_conflict_free_idx(2*thid)];
output[2*globalThid+1].w = temp3[bank_conflict_free_idx(2*thid+1)];
}
}
The code above is a modification of the prefix sum algorithm we discussed in the previous chapter. Here, I'll focus on explaining the modifications. Let's start with the input and output:
@binding(0) @group(0) var<storage, read> input :array<u32>;
@binding(1) @group(0) var<storage, read_write> output :array<vec4<u32>>;
@binding(2) @group(0) var<storage, read_write> sums: array<u32>;
The input array remains the same, but the output now stores vec4 vectors. Since we are using the quaternary numeral system, the vector stores the sums for digits 0, 1, 2, and 3. Additionally, we have a sums array to keep track of the total counts of all digits within each chunk.
@binding(0) @group(1) var<uniform> radixMaskId:u32;
Next, we define the radixMaskId, which indicates the current digit we should focus on. Given that our key is in the format uint32 and we are using the quaternary numeral system, we have 16 possible digits. Therefore, the value of radixMaskId ranges from 0 to 15. Using radixMaskId, we can calculate the mask with the following formula:
var mask:u32 = u32(3) << (radixMaskId << 1);
Next, we define a set of temporary arrays for calculations:
const n:u32 = 512;
var<workgroup> temp0: array<u32,532>;
var<workgroup> temp1: array<u32,532>;
var<workgroup> temp2: array<u32,532>;
var<workgroup> temp3: array<u32,532>;
The following step is to load the values into the temporary arrays. We extract the current digit of interest, and based on the digit's value, we set the corresponding location in the temporary array to 1, indicating one occurrence.
var thid:u32 = LocalInvocationID.x;
var globalThid:u32 = GlobalInvocationID.x;
var mask:u32 = u32(3) << (radixMaskId << 1);
if (thid < (n>>1)){
var val:u32 = (input[2*globalThid] & mask) >> (radixMaskId << 1);
if (val == 0) {
temp0[bank_conflict_free_idx(2*thid)] = 1;
}
else if (val == 1) {
temp1[bank_conflict_free_idx(2*thid)] = 1;
}
else if (val == 2) {
temp2[bank_conflict_free_idx(2*thid)] = 1;
}
else if (val == 3) {
temp3[bank_conflict_free_idx(2*thid)] = 1;
}
val = (input[2*globalThid+1] & mask) >> (radixMaskId << 1);
if (val == 0) {
temp0[bank_conflict_free_idx(2*thid+1)] = 1;
}
else if (val == 1) {
temp1[bank_conflict_free_idx(2*thid+1)] = 1;
}
else if (val == 2) {
temp2[bank_conflict_free_idx(2*thid+1)] = 1;
}
else if (val == 3) {
temp3[bank_conflict_free_idx(2*thid+1)] = 1;
}
}
workgroupBarrier();
The following logic is similar to the prefix sum program, with the key difference being that we perform it on the four temporary arrays. Once the prefix sums are calculated, we need to get the overall counts of the digits in this chunk. Since our prefix sum doesn't include the last value, we need to retrieve the last element of the prefix sum array, count the last input element, and save the result into the sums array. Note that we only ask the first thread of this workgroup to perform the saving operation since each workgroup only produces one set of these values.
if (thid == 0) {
var count0:u32 = temp0[bank_conflict_free_idx(2*255)];
var count1:u32 = temp1[bank_conflict_free_idx(2*255)];
var count2:u32 = temp2[bank_conflict_free_idx(2*255)];
var count3:u32 = temp3[bank_conflict_free_idx(2*255)];
var last:u32 = (input[2*((WorkgroupID.x+1) * 256-1)] & mask) >> (radixMaskId << 1);
switch(last) {
case 0: {count0 += 1;}
case 1: {count1 += 1;}
case 2: {count2 += 1;}
case 3: {count3 += 1;}
default {}
}
last = (input[2*((WorkgroupID.x+1) * 256-1)+1] & mask) >> (radixMaskId << 1);
switch(last) {
case 0: {count0 += 1;}
case 1: {count1 += 1;}
case 2: {count2 += 1;}
case 3: {count3 += 1;}
default {}
}
sums[WorkgroupID.x * 4] = count0;
sums[WorkgroupID.x * 4+1] = count1;
sums[WorkgroupID.x * 4+2] = count2;
sums[WorkgroupID.x * 4+3] = count3;
}
The second pass involves another prefix sum, where we take the sums array generated in the previous pass and calculate its prefix sum. This pass follows a standard approach, so I will skip the detailed explanation. For simplicity, we assume that the number of chunks is less than 512, allowing us to perform the second pass with a single workgroup. This essentially limits the maximum array size we can process to 512x512.
The third pass is the shuffling pass. During this pass, we calculate each element's location in the sorted array and assign the corresponding digit value to the result array.
@binding(0) @group(0) var<storage, read> input :array<u32>;
@binding(1) @group(0) var<storage, read> inputId :array<u32>;
@binding(2) @group(0) var<storage, read> temp :array<vec4<u32>>;
@binding(3) @group(0) var<storage, read> sums: array<u32>;
@binding(4) @group(0) var<uniform> sumSize: u32;
@binding(5) @group(0) var<storage, read_write> output :array<u32>;
@binding(6) @group(0) var<storage, read_write> outputId :array<u32>;
const n:u32 = 512;
@binding(0) @group(1) var<uniform> radixMaskId:u32;
@compute @workgroup_size(256)
fn main(@builtin(global_invocation_id) GlobalInvocationID : vec3<u32>,
@builtin(local_invocation_id) LocalInvocationID: vec3<u32>,
@builtin(workgroup_id) WorkgroupID: vec3<u32>) {
var thid:u32 = LocalInvocationID.x;
var globalThid:u32 = GlobalInvocationID.x;
var mask:u32 = u32(3) << (radixMaskId << 1);
var count0beforeCurrentWorkgroup:u32 = 0;
var count1beforeCurrentWorkgroup:u32 = 0;
var count2beforeCurrentWorkgroup:u32 = 0;
var count3beforeCurrentWorkgroup:u32 = 0;
if (WorkgroupID.x > 0) {
count0beforeCurrentWorkgroup = sums[(WorkgroupID.x-1) * 4];
count1beforeCurrentWorkgroup = sums[(WorkgroupID.x-1) * 4+1];
count2beforeCurrentWorkgroup = sums[(WorkgroupID.x-1) * 4+2];
count3beforeCurrentWorkgroup = sums[(WorkgroupID.x-1) * 4+3];
}
var count0overall:u32 = sums[(sumSize-1)*4];
var count1overall:u32 = sums[(sumSize-1)*4+1];
var count2overall:u32 = sums[(sumSize-1)*4+2];
var count3overall:u32 = sums[(sumSize-1)*4+3];
if (thid < (n>>1)){
var val:u32 = (input[2*globalThid] & mask) >> (radixMaskId << 1);
var id:u32 = 0;
if (val == 0) {
id += temp[2*globalThid].x + count0beforeCurrentWorkgroup;
}
else if (val == 1) {
id +=count0overall;
id += temp[2*globalThid].y + count1beforeCurrentWorkgroup;
}
else if (val == 2) {
id += count0overall;
id += count1overall;
id += temp[2*globalThid].z + count2beforeCurrentWorkgroup;
}
else if (val == 3) {
id +=count0overall;
id +=count1overall;
id +=count2overall;
id += temp[2*globalThid].w +count3beforeCurrentWorkgroup;
}
output[id] = input[2*globalThid];
outputId[id] = inputId[2*globalThid];
//output[2*globalThid] = id;
id = 0;
val = (input[2*globalThid+1] & mask) >> (radixMaskId << 1);
if (val == 0) {
id += temp[2*globalThid+1].x + count0beforeCurrentWorkgroup;
}
else if (val == 1) {
id +=count0overall;
id += temp[2*globalThid+1].y + count1beforeCurrentWorkgroup;
}
else if (val == 2) {
id += count0overall;
id += count1overall;
id += temp[2*globalThid+1].z + count2beforeCurrentWorkgroup;
}
else if (val == 3) {
id +=count0overall;
id +=count1overall;
id +=count2overall;
id += temp[2*globalThid+1].w+ count3beforeCurrentWorkgroup ;
}
output[id] = input[2*globalThid+1];
outputId[id] = inputId[2*globalThid+1];
//output[2*globalThid+1] = id;
}
}
Now let's look at the JavaScript side and see how we set up the input data and trigger the compute shader.
let testArray = [];
let testIdArray = [];
{
//load data
const objResponse = await fetch('../data/dummy.json');
testArray = await objResponse.json();
}
const actualArraySize = testArray.length; // 81946;//512*2+10;
const paddedArraySize = Math.ceil(actualArraySize / 512) * 512;
const chunkCount = Math.ceil(paddedArraySize / 512);
let sumSize = roundUpToNearestPowOf2(chunkCount);
console.log("pos", Number.POSITIVE_INFINITY)
for (let i = 0; i < paddedArraySize; ++i) {
if (i < actualArraySize) {
// testArray.push(Math.floor(random() * 0xFFFFFFFE));
} else {
testArray.push(0xFFFFFFFF);
}
testIdArray.push(i);
}
The testArray is our input array. Instead of generating a random array, the input data is read from a file created during debugging the previous chapter's sample. You can think of it as a random array. We have two array sizes: actualArraySize, which is the true size of the input array, and paddedArraySize, which is the array size rounded up to the nearest multiple of 512. This is because a single workgroup can sort an array of 512 elements.
We also have a chunkCount variable representing the number of workgroups or chunks. As previously mentioned, the digit counts in each chunk will be accumulated in the second prefix sum pass. The sumSize is rounded to the nearest power of two, necessary for calculating the parallel prefix sum using a binary tree structure.
For the padded values, we assign them a large number 0xFFFFFFFF to ensure they appear at the end of the sorted array. The next step involves setting up a series of GPU buffers to hold the input and output arrays, which I will skip as they are straightforward.
We also need to set up the radix mask:
let radixIdUniformBuffers = [];
for (let i = 0; i < 16; ++i) {
let radixIdUniformBuffer = createGPUBuffer(device, new Uint32Array([i]), GPUBufferUsage.UNIFORM);
radixIdUniformBuffers.push(radixIdUniformBuffer);
}
Since we are using the quaternary numeral system, each time we look at two binary digits. Our mask is 0b11, which is shifted left according to the position of the radix. Instead of directly encoding the masks, we encode the positions of the masks. For an unsigned 32-bit integer, there are 16 digit positions. Therefore, we set the radixId to range from 0 to 15. We encode these positions into separate GPU buffers so that during calculation, we can specify the radixId easily by loading the corresponding uniform buffer.
Finally, let's look at how the three passes are triggered:
const commandEncoder = device.createCommandEncoder();
if (hasTimestampQuery) {
commandEncoder.writeTimestamp(querySet, 0);// Initial timestamp
}
for (let i = 0; i < 16; ++i) {
const passEncoder = commandEncoder.beginComputePass(
computePassDescriptor
);
passEncoder.setPipeline(pass1ComputePipeline);
if (i % 2 == 0) {
passEncoder.setBindGroup(0, pass1UniformBindGroupInputOutput0);
}
else {
passEncoder.setBindGroup(0, pass1UniformBindGroupInputOutput1);
}
passEncoder.setBindGroup(1, pass13UniformBindGroupRadixIds[i]);
passEncoder.dispatchWorkgroups(chunkCount);
passEncoder.end();
const pass2Encoder = commandEncoder.beginComputePass(computePassDescriptor);
pass2Encoder.setPipeline(pass2ComputePipeline);
pass2Encoder.setBindGroup(0, pass2UniformBindGroup);
pass2Encoder.dispatchWorkgroups(1);
pass2Encoder.end();
const pass3Encoder = commandEncoder.beginComputePass(computePassDescriptor);
pass3Encoder.setPipeline(pass3ComputePipeline);
if (i % 2 == 0) {
pass3Encoder.setBindGroup(0, pass3UniformBindGroup0);
} else {
pass3Encoder.setBindGroup(0, pass3UniformBindGroup1);
}
pass3Encoder.setBindGroup(1, pass13UniformBindGroupRadixIds[i]);
pass3Encoder.dispatchWorkgroups(chunkCount);
pass3Encoder.end();
}
We loop 16 times because we have 16 radix positions. Each iteration accomplishes three passes. For the first and third passes, we alternate the roles of the input and output arrays to improve efficiency and avoid unnecessary data copying. Finally, we read back the sorted array, but I will skip the details.