2.2 Implementing Gaussian Blur
2D image processing is an excellent use case for WebGPU. In this tutorial, we will implement one of the most common 2D image filters: Gaussian blur. While a naive implementation is straightforward, we will aim to create an optimized version through five iterations of incremental improvements.
For 2D image processing, we typically render the image to be processed on a screen-aligned rectangle. The general setup should already be familiar, so we will not repeat it here. Instead, we will focus on the blur algorithm implemented in the fragment shader. Please refer to the sample code for detailed pipeline setup and other specifics.
Let's start with the most basic version. This initial version isn't truly Gaussian blur yet; it calculates an average of the nearby colors for each pixel, which is often called a box blur. In contrast, a full Gaussian blur calculates a weighted average based on a Gaussian kernel.
Launch Playground - 2_02_1_blur_1Since the JavaScript setup is quite similar to the texture mapping tutorial and many other previous samples, I will skip repeatedly showing what we already know. The focus of this tutorial is mainly on the fragment shader, where the algorithm is primarily implemented.
@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4<f32> {
const kernelSize = 8.0;
var color = vec4<f32>(0.0, 0.0, 0.0, 0.0);
var intensity: f32 = 0.0;
for(var y: f32 = - kernelSize; y <= kernelSize; y+=1.0) {
let offsettedY = y + in.pixel_coord.y;
if (offsettedY >= 0.0 && offsettedY <= img_size.y ) {
for (var x: f32 = -kernelSize; x<=kernelSize; x+=1.0) {
let offsettedX = x + in.pixel_coord.x;
if (offsettedX >= 0.0 && offsettedX <= img_size.x) {
let tex_coord = vec2(offsettedX / img_size.x, offsettedY / img_size.y);
let c = textureSampleLevel(t_diffuse, s_diffuse, tex_coord,0);
color += c;
intensity += 1.0;
}
}
}
}
color /= intensity;
color.w = 1.0;
return color;
}
The general idea of the basic version is simple: for each pixel, we look at its nearby 15x15 window. We fetch all pixels from this window and calculate the average color. Recall that previously we mentioned the textureSample function must be called in a uniform control flow. Here, we are using a slightly different variant, called textureSampleLevel, which is not in a uniform control flow. What's the difference?
The textureSampleLevel function requires one additional parameter compared to textureSample: a level ID. Consequently, textureSampleLevel does not perform mipmapping but requires an explicit level index. The logic in textureSample that determines the correct mipmap levels is what necessitates uniform control flow. If we do not need mipmapping, we can sample textures outside of uniform control flow. We will explain why determining the right mipmap level requires uniformity in a future chapter.
Now, let's look at an improved version:
Launch Playground - 2_02_2_blur_2@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4<f32> {
const kernelSize = 8.0;
var color = vec4<f32>(0.0, 0.0, 0.0, 0.0);
var intensity: f32 = 0.0;
const sigma = 8.0;
const PI = 3.1415926538;
for(var y: f32 = - kernelSize; y <= kernelSize; y+=1.0) {
let offsettedY = y + in.pixel_coord.y;
if (offsettedY >= 0.0 && offsettedY <= img_size.y ) {
for (var x: f32 = -kernelSize; x<=kernelSize; x+=1.0) {
let offsettedX = x + in.pixel_coord.x;
if (offsettedX >= 0.0 && offsettedX <= img_size.x) {
let tex_coord = vec2(offsettedX / img_size.x, offsettedY / img_size.y);
let gaussian_v = 1.0 / (2.0 * PI * sigma * sigma) * exp(-(x*x + y*y) / (2.0 * sigma * sigma));
let c = textureSampleLevel(t_diffuse, s_diffuse, tex_coord,0);
color += c * gaussian_v;
intensity += gaussian_v;
}
}
}
}
color /= intensity;
color.w = 1.0;
return color;
}
This version is not that different from the previous one, but now we are applying a weight to each color. The weight is based on the Gaussian value given the distance of each pixel to the center pixel, ensuring that closer texels contribute more to the final color than those further away.
Recall the equation of a 2D Gaussian:
G(x,y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
The problem with the above version is that for each fragment, we are recalculating the Gaussian values. This is unnecessary because the 15x15 window is the same for all fragments. The Gaussian values for each pixel in the 15x15 window are solely determined by their distances to the center, making the values identical across all fragments. Therefore, we should calculate the Gaussian weights once and cache them in a lookup table. By doing this, we can retrieve the Gaussian weights instead of recalculating them repeatedly. Let's modify our code accordingly.
@group(0) @binding(2)
var<uniform> img_size: vec2<f32>;
//texture doesn't need <uniform>, because it is non-host-sharable (what does it mean?)
@group(0) @binding(3)
var t_diffuse: texture_2d<f32>;
@group(0) @binding(4)
var s_diffuse: sampler;
@group(0) @binding(5)
var<storage> kernel: array<f32>;
@group(0) @binding(6)
var<uniform> kernel_size: f32;
@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4<f32> {
var color = vec4<f32>(0.0, 0.0, 0.0, 0.0);
var intensity: f32 = 0.0;
for(var y: f32 = - kernel_size; y <= kernel_size; y+=1.0) {
let offsettedY = y + in.pixel_coord.y;
if (offsettedY >= 0.0 && offsettedY <= img_size.y ) {
for (var x: f32 = -kernel_size; x<=kernel_size; x+=1.0) {
let offsettedX = x + in.pixel_coord.x;
if (offsettedX >= 0.0 && offsettedX <= img_size.x) {
let indexY = u32(y + kernel_size);
let indexX = u32(x + kernel_size);
let index = indexY * (u32(kernel_size) * 2 + 1) + indexX;
let tex_coord = vec2(offsettedX / img_size.x, offsettedY / img_size.y);
let gaussian_v = kernel[index];
let c = textureSampleLevel(t_diffuse, s_diffuse, tex_coord,0);
color += c * gaussian_v;
intensity += gaussian_v;
}
}
}
}
color /= intensity;
color.w = 1.0;
return color;
}
The Gaussian weights are calculated in JavaScript and passed in as a storage array. This is the first time we have encountered a storage array. We use a storage buffer because the size of the weight array is related to the window size, and we want it to be flexible so that the window size can be adjusted. Consequently, the array size can't be predetermined. Runtime-sized arrays can only be used in the storage address space, not in the uniform address space, making the storage buffer the appropriate choice here. Storage buffers offer additional benefits, such as supporting write-back values from a shader. We will explore more uses of storage buffers in future tutorials.
let kValues = []
const kernelSize = 8.0;
const sigma = 8.0;
let intensity = 0.0;
for (let y = - kernelSize; y <= kernelSize; y += 1.0) {
for (let x = -kernelSize; x <= kernelSize; x += 1.0) {
let gaussian_v = 1.0 / (2.0 * Math.PI * sigma * sigma) * Math.exp(-(x * x + y * y) / (2.0 * sigma * sigma));
intensity += gaussian_v;
kValues.push(gaussian_v);
}
}
const kernelBuffer = new Float32Array(kValues);
const kernelBufferStorageBuffer = createGPUBuffer(device, kernelBuffer, GPUBufferUsage.STORAGE);
const kernelSizeBuffer = new Float32Array([kernelSize]);
const kernelBufferSizeUniformBuffer = createGPUBuffer(device, kernelSizeBuffer, GPUBufferUsage.UNIFORM);
let uniformBindGroupLayout = device.createBindGroupLayout({
entries: [
{
binding: 0,
visibility: GPUShaderStage.VERTEX,
buffer: {}
},
{
binding: 1,
visibility: GPUShaderStage.VERTEX,
buffer: {}
},
{
binding: 2,
visibility: GPUShaderStage.FRAGMENT,
buffer: {}
},
{
binding: 3,
visibility: GPUShaderStage.FRAGMENT,
texture: {}
},
{
binding: 4,
visibility: GPUShaderStage.FRAGMENT,
sampler: {}
},
{
binding: 5,
visibility: GPUShaderStage.FRAGMENT,
buffer: {
type: 'read-only-storage'
}
},
{
binding: 6,
visibility: GPUShaderStage.FRAGMENT,
buffer: {}
}
]
});
let uniformBindGroup = device.createBindGroup({
layout: uniformBindGroupLayout,
entries: [
{
binding: 0,
resource: {
buffer: translateMatrixUniformBuffer
}
},
{
binding: 1,
resource: {
buffer: projectionMatrixUniformBuffer
}
},
{
binding: 2,
resource: {
buffer: imgSizeUniformBuffer
}
},
{
binding: 3,
resource: texture.createView()
},
{
binding: 4,
resource:
sampler
},
{
binding: 5,
resource: {
buffer: kernelBufferStorageBuffer
}
},
{
binding: 6,
resource: {
buffer: kernelBufferSizeUniformBuffer
}
}
]
});
The code snippet above shows how we populate the kernel data in JavaScript. Notice that the usage is set to STORAGE to match the storage address space specified in the shader. When defining the uniformBindGroupLayout, we need to specify type: read-only-storage. The 2D Gaussian kernel is unrolled into a 1D array. Inside the shader, we recover the 1D access index from the xy coordinates. The kernelSize defines the window size, with windowSize = 2 * kernelSize + 1.
The problem with the code snippet we've seen so far is that for each fragment, we have to loop 15x15 times. This involves a significant amount of calculation, especially when multiplied by the number of pixels. To further optimize it, we need to reduce the number of loop iterations.
\begin{aligned}
G(x,y) &= \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
G(x,y) &= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}\times \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{y^2}{2\sigma^2}}
\end{aligned}
If we inspect the equation for the 2D Gaussian, we see that it can be separated into a multiplication. By taking the left column of the Gaussian kernel as an example, we can calculate it by first treating it as a 1D Gaussian and calculating the vertical weighted sum for each texel. Then, we multiply it by the horizontal Gaussian: \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}. Hence, we can break the calculation down into two passes. During the first pass, we calculate the 1D Gaussian blur vertically, and during the second pass, we do it horizontally. The end result is the same as calculating it in a 15x15 window.
The benefit of this approach is that we significantly reduce the number of loops. To calculate the vertical 1D Gaussian, we only need to loop 15 times. Adding the 15 loops for the horizontal calculation, we only need to loop 30 times in total, compared to the 15x15 (225) times previously. This is a substantial saving.
However, this optimization requires two passes with two shaders:
@group(0) @binding(0)
var<uniform> img_size: vec2<f32>;
//texture doesn't need <uniform>, because it is non-host-sharable (what does it mean?)
@group(0) @binding(1)
var t_diffuse: texture_2d<f32>;
@group(0) @binding(2)
var s_diffuse: sampler;
@group(0) @binding(3)
var<storage> kernel: array<f32>;
@group(0) @binding(4)
var<uniform> kernel_size: f32;
@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4<f32> {
var color = vec4<f32>(0.0, 0.0, 0.0, 0.0);
var intensity: f32 = 0.0;
for(var y: f32 = - kernel_size; y <= kernel_size; y+=1.0) {
let offsettedY = y + in.pixel_coord.y;
if (offsettedY >= 0.0 && offsettedY <= img_size.y ) {
let indexY = u32(y + kernel_size);
let tex_coord = vec2(in.pixel_coord.x / img_size.x, offsettedY / img_size.y);
let gaussian_v = kernel[indexY];
let c = textureSampleLevel(t_diffuse, s_diffuse, tex_coord,0);
color += c * gaussian_v;
intensity += gaussian_v;
}
}
color /= intensity;
color.w = 1.0;
return color;
}
and horizontal:
@group(0) @binding(2)
var<uniform> img_size: vec2<f32>;
@group(0) @binding(3)
var v_result: texture_2d<f32>;
@group(0) @binding(4)
var s_diffuse: sampler;
@group(0) @binding(5)
var<storage> kernel: array<f32>;
@group(0) @binding(6)
var<uniform> kernel_size: f32;
@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4<f32> {
var color = vec4<f32>(0.0, 0.0, 0.0, 0.0);
var intensity: f32 = 0.0;
for(var x: f32 = - kernel_size; x <= kernel_size; x+=1.0) {
let offsettedX = x + in.pixel_coord.x;
if (offsettedX >= 0.0 && offsettedX <= img_size.x ) {
let indexX = u32(x + kernel_size);
let tex_coord = vec2(offsettedX / img_size.x, in.pixel_coord.y / img_size.y);
let gaussian_v = kernel[indexX];
let c = textureSampleLevel(v_result, s_diffuse, tex_coord,0);
color += c * gaussian_v;
intensity += gaussian_v;
}
}
color /= intensity;
color.w = 1.0;
return color;
}
The kernel passed into the shader is also slightly different:
let kValues = []
const kernelSize = 8.0;
const sigma = 8.0;
let intensity = 0.0;
for (let y = - kernelSize; y <= kernelSize; y += 1.0) {
let gaussian_v = 1.0 / Math.sqrt(2.0 * Math.PI * sigma * sigma) * Math.exp(-(y * y) / (2.0 * sigma * sigma));
intensity += gaussian_v;
kValues.push(gaussian_v);
}
const kernelBuffer = new Float32Array(kValues);
const kernelBufferStorageBuffer = createGPUBuffer(device, kernelBuffer, GPUBufferUsage.STORAGE);
const kernelSizeBuffer = new Float32Array([kernelSize]);
const kernelBufferSizeUniformBuffer = createGPUBuffer(device, kernelSizeBuffer, GPUBufferUsage.UNIFORM);
We need to create two pipelines for these shaders and launch them consecutively. The first pass calculates the vertical results and caches them in a temporary texture map. The second pass builds on the first pass's results to produce the final output.
const pipelineLayoutDescPass1 = { bindGroupLayouts: [uniformBindGroupLayoutPass1] };
const pipelineLayoutPass1 = device.createPipelineLayout(pipelineLayoutDescPass1);
const colorStatePass1 = {
format: 'rgba8unorm'
};
const pipelineDescPass1 = {
layout: pipelineLayoutPass1,
vertex: {
module: shaderModuleVertical,
entryPoint: 'vs_main',
buffers: [pixelCoordsBufferLayoutDescPass1]
},
fragment: {
module: shaderModuleVertical,
entryPoint: 'fs_main',
targets: [colorStatePass1]
},
primitive: {
topology: 'triangle-strip',
frontFace: 'ccw',
cullMode: 'none'
}
};
const pipelinePass1 = device.createRenderPipeline(pipelineDescPass1);
let colorAttachmentPass1 = {
view: pass1texture.createView(),
clearValue: { r: 0, g: 0, b: 0, a: 0 },
loadOp: 'clear',
storeOp: 'store'
};
const renderPassDescPass1 = {
colorAttachments: [colorAttachmentPass1]
};
commandEncoder = device.createCommandEncoder();
passEncoder = commandEncoder.beginRenderPass(renderPassDescPass1);
passEncoder.setViewport(0, 0, texture.width, texture.height, 0, 1);
passEncoder.setPipeline(pipelinePass1);
passEncoder.setBindGroup(0, uniformBindGroupPass1);
passEncoder.setVertexBuffer(0, pixelCoordsBuffer);
passEncoder.draw(4, 1);
passEncoder.end();
let uniformBindGroupPass2 = device.createBindGroup({
layout: uniformBindGroupLayoutPass2,
entries: [
{
binding: 0,
resource: {
buffer: translateMatrixUniformBuffer
}
},
{
binding: 1,
resource: {
buffer: projectionMatrixUniformBuffer
}
},
{
binding: 2,
resource: {
buffer: imgSizeUniformBuffer
}
},
{
binding: 3,
resource: pass1texture.createView()
},
{
binding: 4,
resource:
sampler
},
{
binding: 5,
resource: {
buffer: kernelBufferStorageBuffer
}
},
{
binding: 6,
resource: {
buffer: kernelBufferSizeUniformBuffer
}
}
]
});
const pipelineLayoutDescPass2 = { bindGroupLayouts: [uniformBindGroupLayoutPass2] };
const pipelineLayoutPass2 = device.createPipelineLayout(pipelineLayoutDescPass2);
const colorStatePass2 = {
format: 'bgra8unorm'
};
const pipelineDescPass2 = {
layout: pipelineLayoutPass2,
vertex: {
module: shaderModuleHorizontal,
entryPoint: 'vs_main',
buffers: [positionBufferLayoutDesc, pixelCoordsBufferLayoutDescPass2]
},
fragment: {
module: shaderModuleHorizontal,
entryPoint: 'fs_main',
targets: [colorStatePass2]
},
primitive: {
topology: 'triangle-strip',
frontFace: 'ccw',
cullMode: 'none'
}
};
const pipelinePass2 = device.createRenderPipeline(pipelineDescPass2);
let pass2texture = context.getCurrentTexture();
let colorAttachmentPass2 = {
view: pass2texture.createView(),
clearValue: { r: 1.0, g: 0.0, b: 0.0, a: 1.0 },
loadOp: 'clear',
storeOp: 'store'
}
const renderPassDescPass2 = {
colorAttachments: [colorAttachmentPass2]
}
let passEncoder2 = commandEncoder.beginRenderPass(renderPassDescPass2);
passEncoder2.setViewport(0, 0, canvas.width, canvas.height, 0, 1);
passEncoder2.setPipeline(pipelinePass2);
passEncoder2.setBindGroup(0, uniformBindGroupPass2);
passEncoder2.setVertexBuffer(0, positionBuffer);
passEncoder2.setVertexBuffer(1, pixelCoordsBuffer);
passEncoder2.draw(4, 1);
passEncoder2.end();
device.queue.submit([commandEncoder.finish()]);
The exact process of creating and launching these two passes is the same as shown in the render-to-texture tutorial.
This is not the end of the optimization, though. There is another opportunity to improve the performance of Gaussian blur by harnessing the bilinear interpolation built into texture map access. If we model a texture as a simple 2D array, accessing each texel would require one texture read. However, a texture map is not exactly the same as a 2D array, as we can sample it using non-integer coordinates. In this case, bilinear interpolation is involved, resulting in a weighted average of the surrounding pixels. For example, if our goal is to get the sum of two nearby texels, we can use one texture read to get the average of the two values by setting our texture read coordinates in the middle of them and scale the value back by 2.
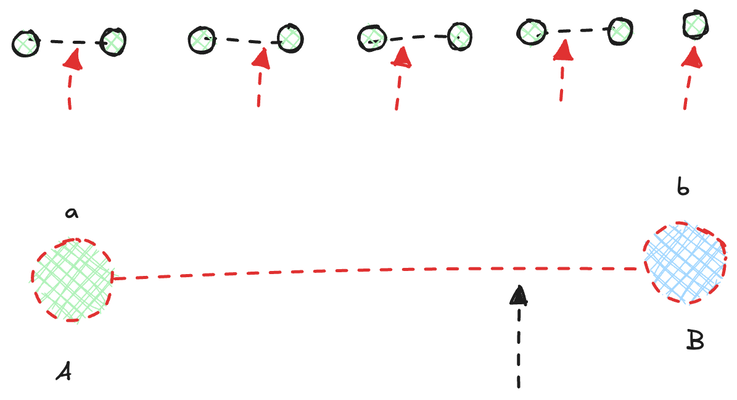
We can be even smarter by incorporating the Gaussian weight values into the formula. For example, in the illustration above, we have a 1D texture map of 9 texels. Each green dot represents a texel. If this were a 1D array, we would need to access it 9 times to retrieve all its values. However, if it is a texture map, we can leverage the built-in interpolations to access two texels at a time. In total, we would only need 5 accesses to get the job done.
The first step is to group nearby texels into pairs. Assuming the color values of these texels are A, B, \ldots, I and their Gaussian weights are a, b, \ldots, i, the value we ultimately want to calculate is:
\frac{aA + bB + ... +iI}{a + b + ... + i}
Let's focus on A and B. By setting the texture coordinate to \frac{b}{a+b}, we can obtain the following sampled value:
\begin{aligned}
v &= \frac{a}{a+b} \times A + (1 - \frac{b}{a+b}) \times B
v &= \frac{aA+bB}{a+b}
\end{aligned}
Since what we want is aA + bB, we just need to scale it back by a+b. We repeat this process for all the two-texel groups, and in the end, we divide the weighted sum by the sum of all Gaussian weights. This approach essentially achieves the same result as accessing the texture 9 times.
The above process is implemented with the following changes:
let kValues = [];
let offsets = [];
const kernelSize = 8.0;
const sigma = 8.0;
let intensity = 0.0;
for (let y = - kernelSize; y <= kernelSize; y += 1.0) {
let gaussian_v = 1.0 / Math.sqrt(2.0 * Math.PI * sigma * sigma) * Math.exp(-(y * y) / (2.0 * sigma * sigma));
intensity += gaussian_v;
kValues.push(gaussian_v);
offsets.push(y);
}
let kValues2 = [];
let offsets2 = [];
let i = 0;
// loop for all 2-texel groups
for (; i < kValues.length - 1; i += 2) {
const A = kValues[i];
const B = kValues[i + 1];
const k = A + B;
const alpha = A / k;
const offset = offsets[i] + alpha;
kValues2.push(k / intensity);
offsets2.push(offset);
}
// if the window size is an odd number, there should be one lingering texel left
if (i < kValues.length) {
const A = kValues[i];
const offset = offsets[i];
kValues2.push(A / intensity);
offsets2.push(offset);
}
In the shader, we introduce two key modifications. First, we use lookups to determine the texture access offsets (coordinates), allowing us to efficiently blend two nearby texels. Second, we incorporate a scale-back factor to adjust the final weighted sum appropriately.
@group(0) @binding(2)
var<uniform> img_size: vec2<f32>;
@group(0) @binding(3)
var v_result: texture_2d<f32>;
@group(0) @binding(4)
var s_diffuse: sampler;
@group(0) @binding(5)
var<storage> weights: array<f32>;
@group(0) @binding(6)
var<storage> offsets: array<f32>;
@group(0) @binding(7)
var<uniform> kernel_size: u32;
@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4<f32> {
var color = vec4<f32>(0.0, 0.0, 0.0, 0.0);
for(var x: u32 = 0; x < kernel_size; x++) {
let offsettedX = offsets[x] + in.pixel_coord.x;
let tex_coord = vec2(offsettedX / img_size.x, in.pixel_coord.y / img_size.y);
// access texture in middle of two samples
let c = textureSampleLevel(v_result, s_diffuse, tex_coord,0);
// scales back by weight
color += c * weights[x];
}
color.w = 1.0;
return color;
}
These changes allow us to achieve the same result as before but with significantly improved performance.
Launch Playground - 2_02_5_blur_5